1. Diffusion models surpass autoregressive models given sufficient compute.
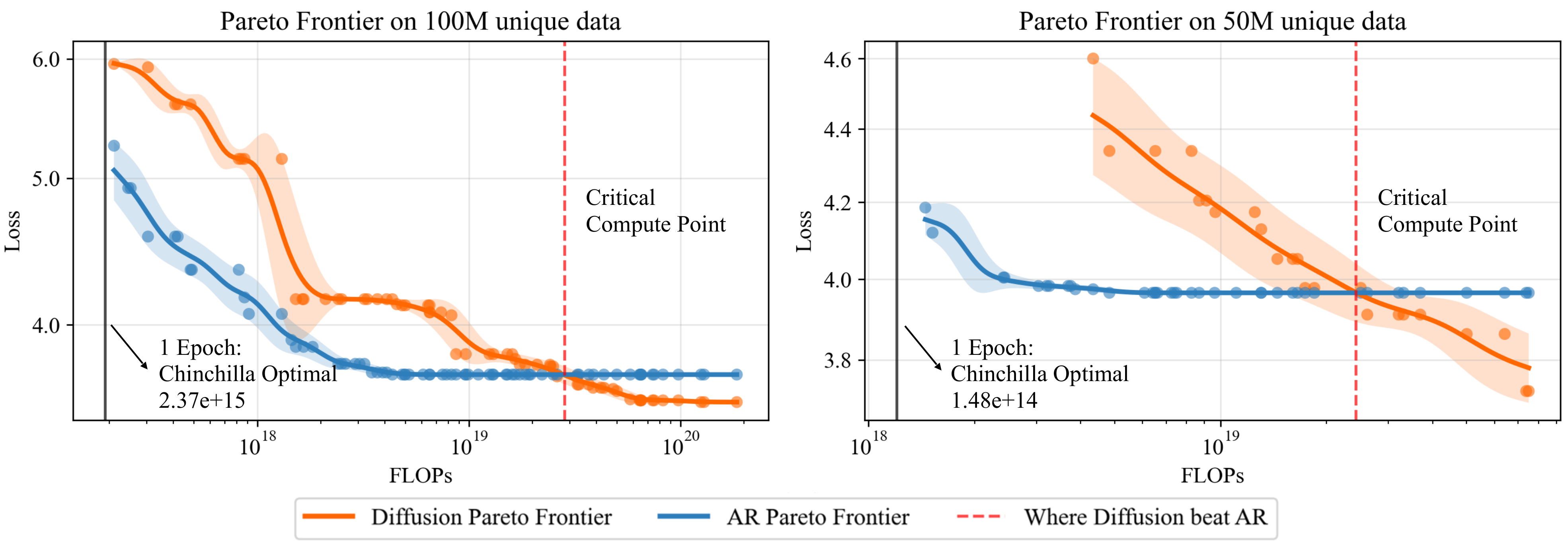
Across a wide range of unique token budgets, AR models initially outperform diffusion models at low compute,
but quickly saturate. Beyond a critical compute threshold, diffusion models continue improving and ultimately
achieve better performance.
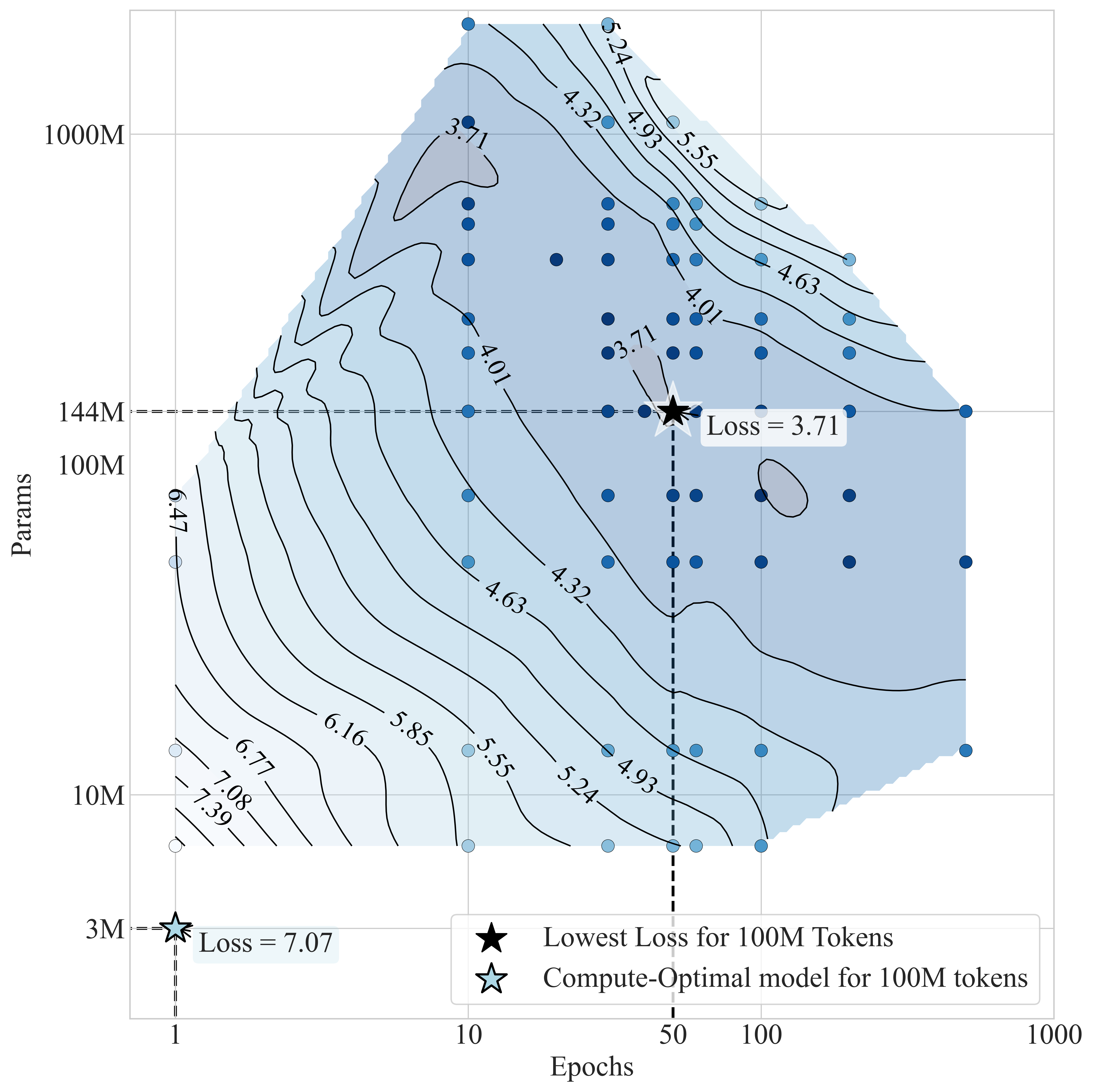
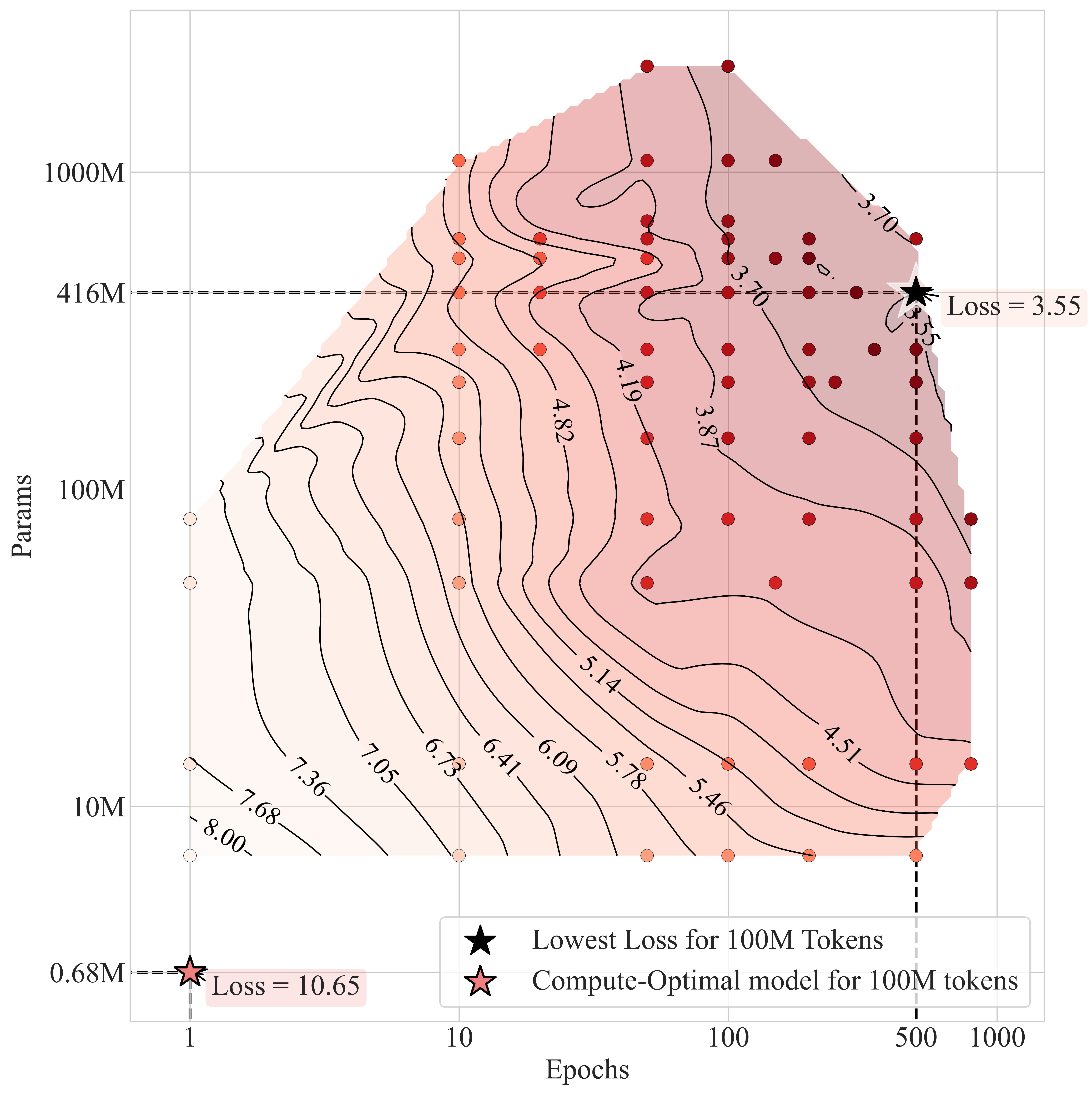
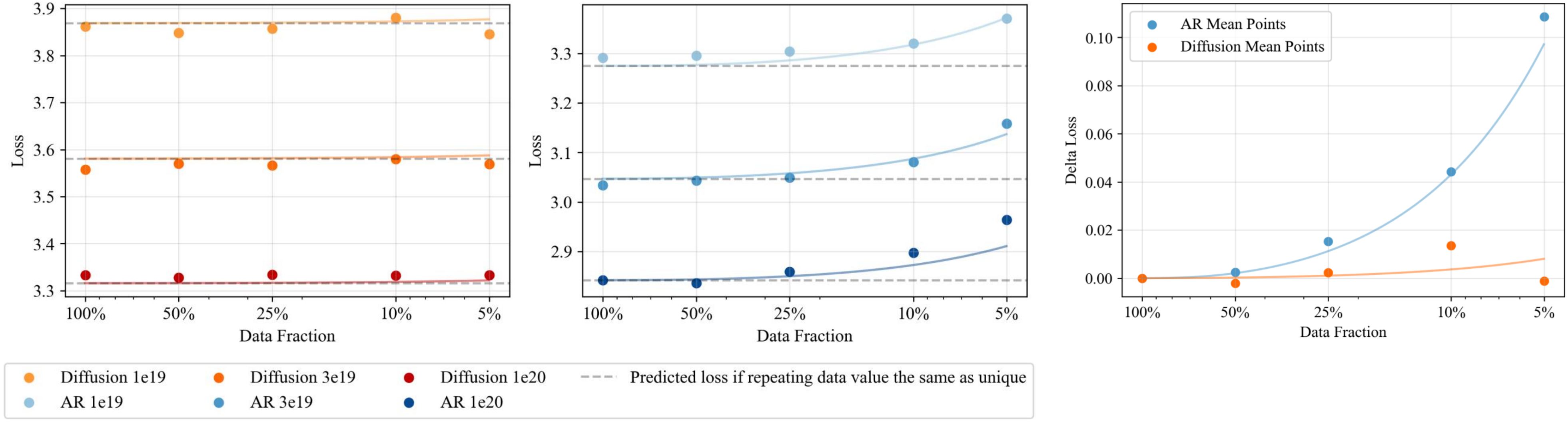
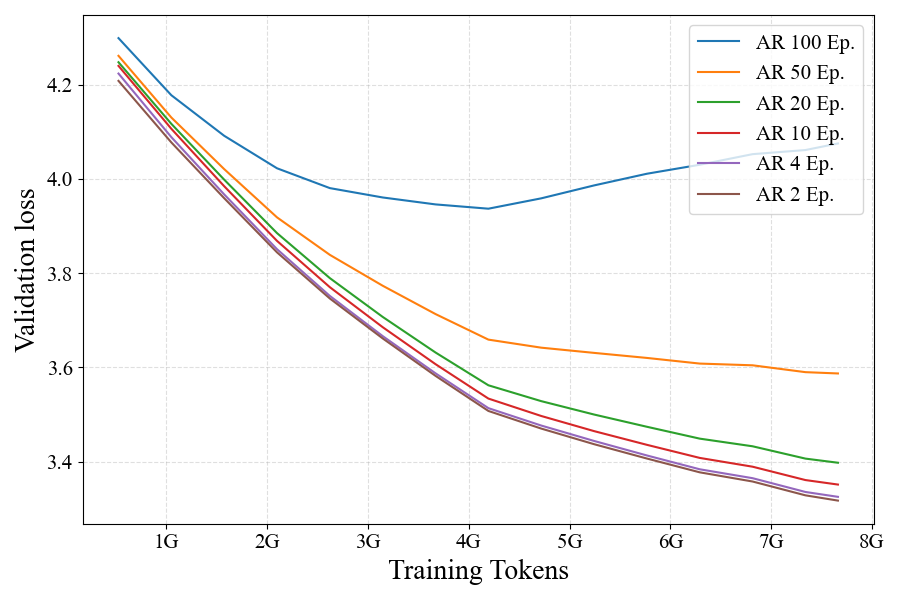
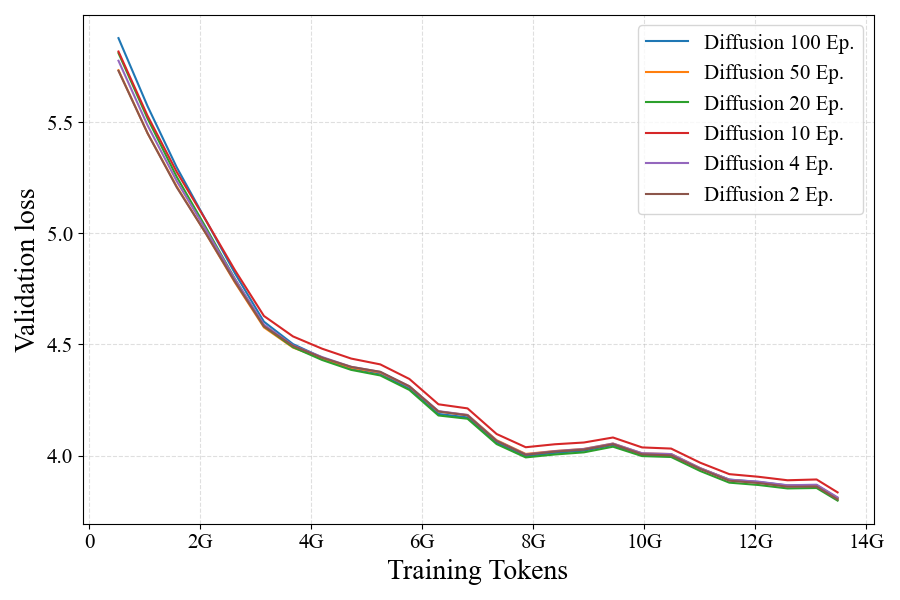
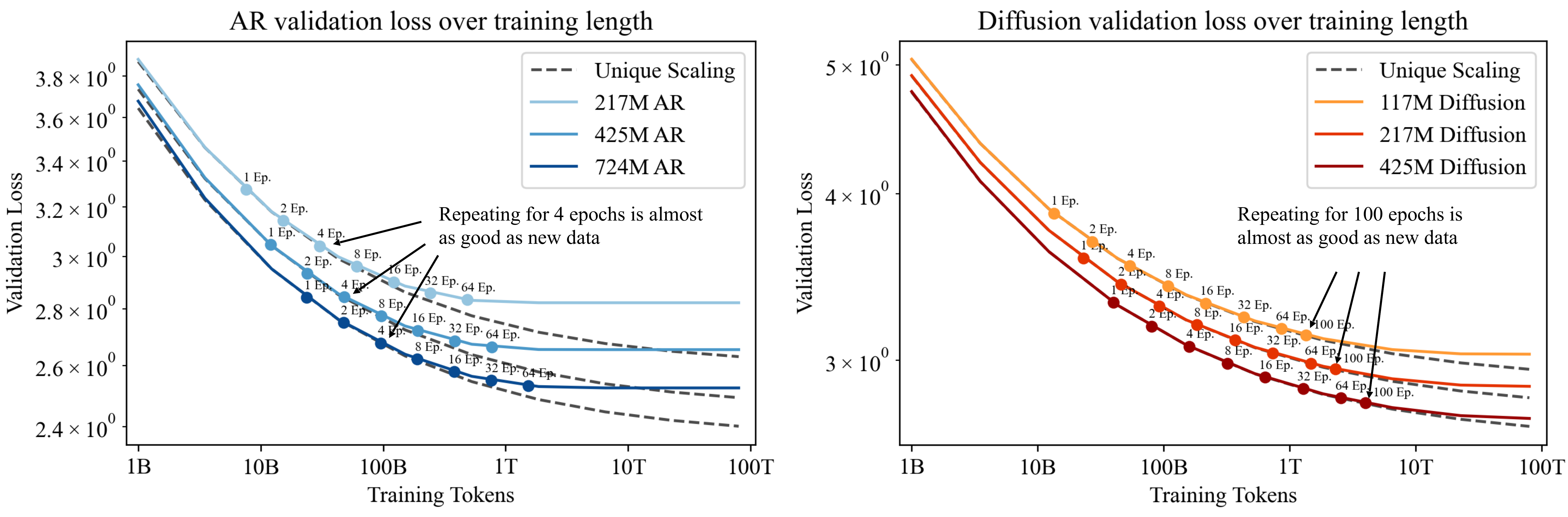
2. Diffusion models benefit far more from repeated data.
While AR models can effectively use repeated data for up to 4 epochs, diffusion models can be trained
on repeated data for up to 100 epochs with repeated data almost as effective as fresh data.
3. Diffusion models have a much higher effective epoch count.
We find \(R_D^* \approx 500\) for diffusion models compared to \(R_D^* \approx 15\) for AR models,
suggesting diffusion models can benefit from repeated data over far more epochs without major degradation.
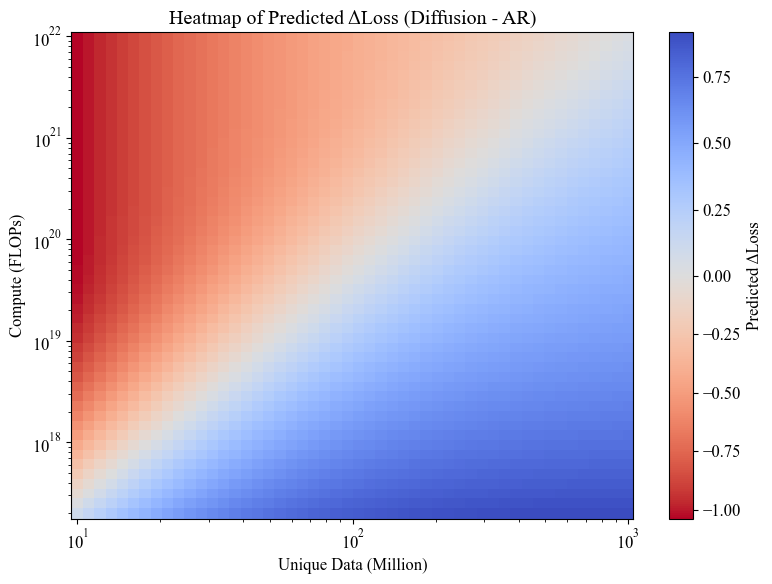
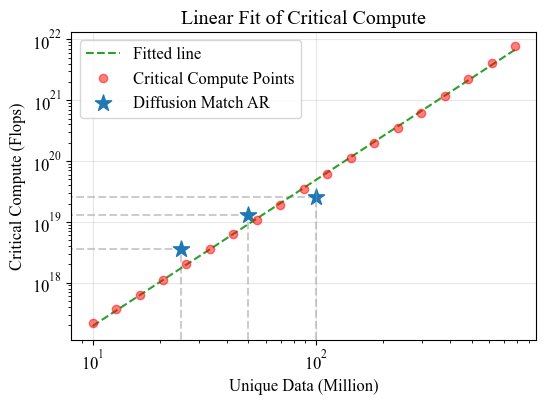
4. Critical compute point follows a power law with dataset size.
We derive a closed-form expression \(C_{\text{crit}}(U) = 2.12 \times 10^{1.956} \cdot U^{2.174}\)
that predicts when diffusion becomes the favorable modeling choice for any given dataset size.
5. Diffusion models yield better downstream performance.
The validation loss improvements translate to consistent gains across diverse downstream language tasks.
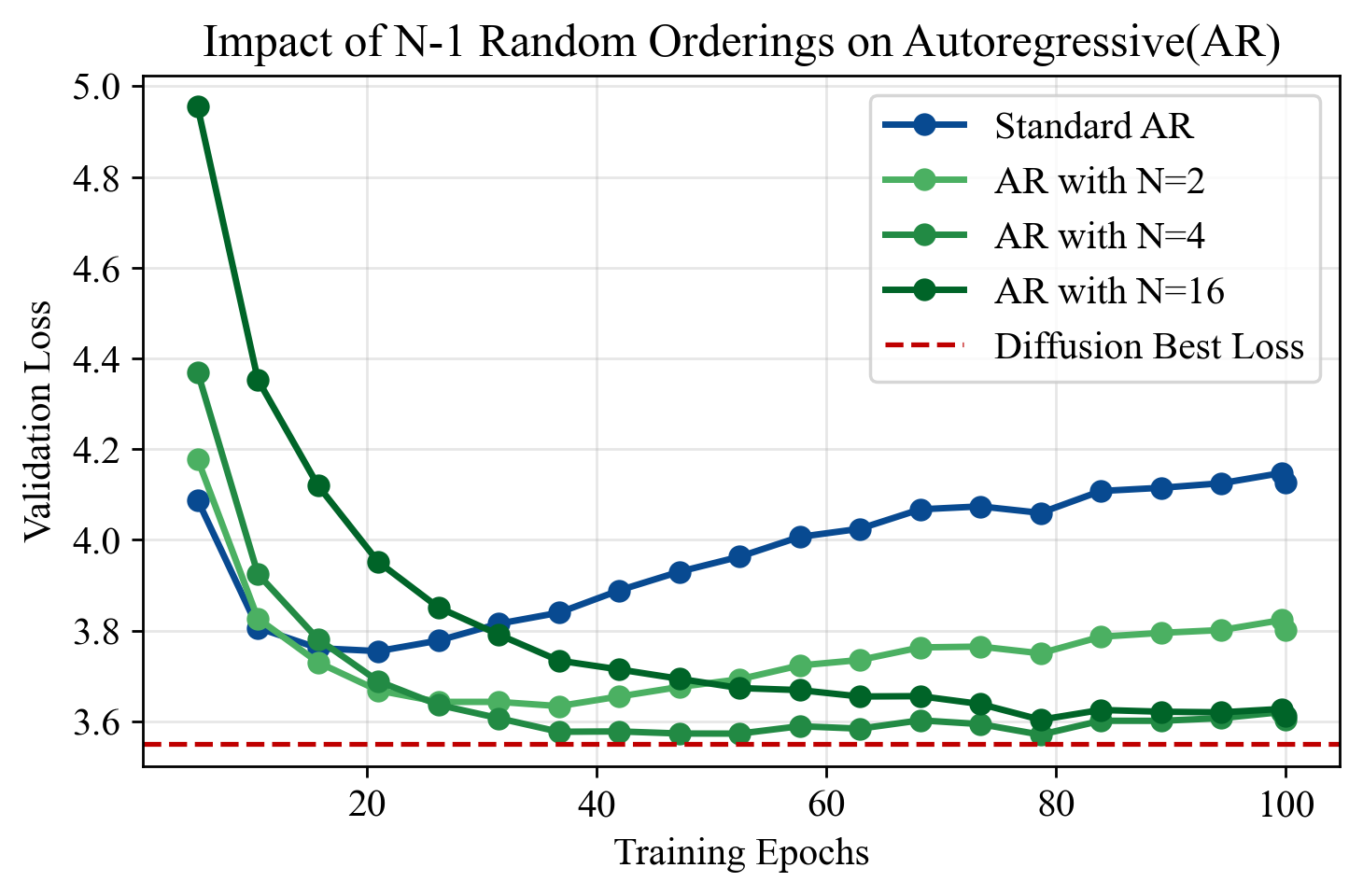
6. Exposure to different token orderings helps explain diffusion's data efficiency.
By adding explicit data augmentations to AR training, we find that diffusion models' advantage arises from their exposure to a diverse set of token orderings.